Cyclotron: A Particle Accelerator

A theoretical research based project on Cyclotron: A particle accelerator.

Cyclotrons are a classification of particle accelerators. Their principal application is to set charged particles into high speed motions, which may even be close to the speed of light and can carry an energy of several billion electron-volts. This form of high energy motion is achieved by subjecting the charged particles into electromagnetic fields and thus accelerating them by applying electromagnetic forces of attraction and repulsion.

Cyclotron is a classification of an electrodynamic particle accelerator. It accelerates the charged particle outward from the through a spiral trajectory by subjecting the charged particle into a static magnetic field and repeatedly accelerates the particle by a rapidly alternating dynamic electric field. The final energy obtained by the particles are much greater than the impressed voltages on the electrodes.

Cyclotron was invented by the American scientist Ernest Orlando Lawrence during the years 1929 and 1930, for which he was awarded The Nobel Prize in Physics in 1939. The first working model of cyclotron was constructed in 1931 by American physicist Milton Stanley Livingston at the University of California at Berkeley; it was a 4-inch working model of cyclotron and was able to produce 80,000 eV protons.

Fig.1 - The first cyclotron
Fig.1 - The first cyclotron

Cyclotron was a breakthrough in particle physics, as it was able to accelerate charged particles to a speed that was not possible otherwise. It paved the way for various researches in fields of physics, chemistry, medical sciences, and in other scientific subjects. Cyclotron was used for various important scientific studies such as the discovery of transmutation of atomic nuclei artificially, the discovery of transuranium elements, research for treating cancer cells, and many more.

Particle Accelerators

A particle accelerator is a device that is used to propel charged particles to extremely high speed and energies using electromagnetic fields, and to contain them in well-defined beams.

There are two major classifications of particle accelerators:

Electrostatic particle accelerators

Electrostatic particle accelerators use static electric fields to accelerate charged particles to high energy speeds. Electrostatic accelerators accelerate particles by applying static electric potential across the particle. As the particle comes in the electric field of the applied potential the particle experiences a force, which results in the acceleration of the particle.

Some examples of electrostatic particle accelerators:

Electrodynamic particle accelerators

Electrodynamic particle accelerator uses a dynamic electric field to accelerate charged particles to high energy speeds. These particle accelerators accelerate particles by subjecting them to oscillating electric potentials. Electrodynamic accelerators can accelerate particles to higher energies compared to electrostatic accelerators.

Some examples of electrodynamic particle accelerators:

Cyclotron: A Particle Accelerator

Cyclotron accelerates a charged particle to remarkably high energy without the use of high voltage, and thus avoiding the limitations of insulation break-down. The charged particles move in widening semi-circular paths in a uniform magnetic field, crossing back and forth in a vacuum chamber between two D- shaped hollow electrodes in resonance with a rapidly oscillatory electric field. The particles moving in a spiral outward trajectory are accelerated at each traversal of the electric field, attaining a final energy hundreds of times greater than that available from the impressed voltage on the electrodes. This principle of resonance acceleration is termed as “magnetic resonance acceleration” and the technical name for the device is “magnetic resonance accelerator”, which is concisely termed as “cyclotron”.

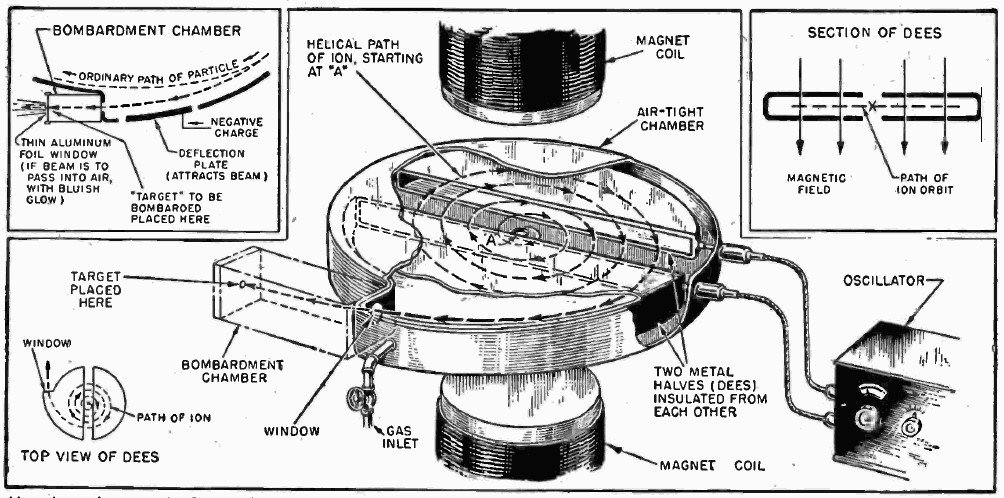
Fig.2 - Construction and working of a cyclotron
Fig.2 - Construction and working of a cyclotron

The cyclotron principle was proposed in 1930 by Professor Ernest Orlando Lawrence of the University of California. The original idea of accelerating a charged particle in an oscillatory electric field was suggested by a experiment conducted by the Norwegian accelerator physicist Rolf Wideröe in 1928 in which ions of sodium and potassium were accelerated to twice the applied voltage in traversing two tubular electrodes in line between which an oscillatory electric field was applied. The conception of the idea of cyclotron occurred to Lawrence in the library of the University of California in the summer of 1929, when professor Lawrence was browsing through the current journals and read Wideröe’s paper in “Archiv für Elektrotechnik”. The principle of the acceleration in a cyclotron was announced in a short article by professor Lawrence and his graduate student Edlefsen in 1930. Edlefsen, on professor Lawrence’s request, attempted a brief preliminary experimental test of the principle but the experiment was not successful in demonstrating resonance and therefore no experimental results could be reported. Later, professor Lawrence suggested this problem to Livingston, a graduate student at Berkeley, as the subject for an experimental research investigation to demonstrate the validity of the resonance principle. A doctorate thesis by Livingston dated April 14, 1931 reported the results of the experiment. This was the first experimental verification of the principle of cyclotron resonance. For this preliminary study only small-sized laboratory equipment was available, including an electromagnet of 4 inches pole diameter. An illustration from the thesis shows the arrangement of the components.

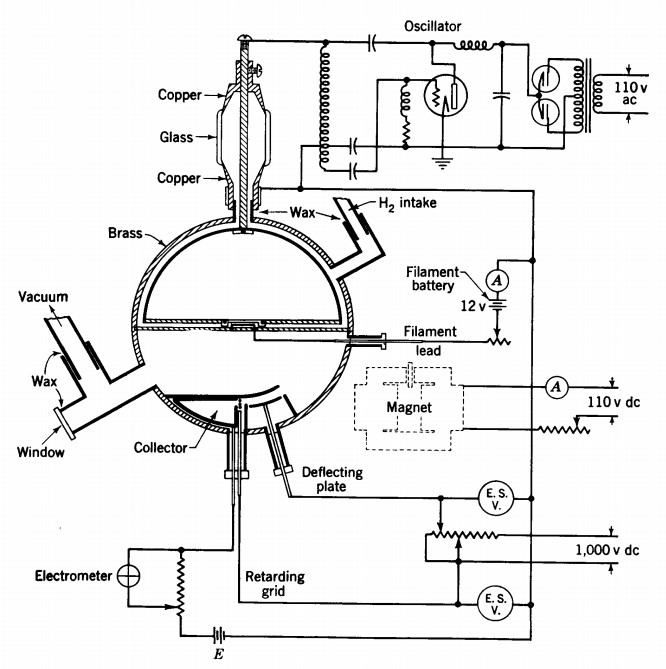
Fig.3 - Illustration of the working of one of the first cyclotrons
Fig.3 - Illustration of the working of one of the first cyclotrons

Basic Principles of Working of a Cyclotron

Static magnetic field

The static magnetic field is produced by a pair of magnets preferably electromagnets. These magnets are aligned horizontally with a specific amount of distance between them which is crucial for the cyclotron to work. It is preferred that the magnets are adjusted in such a manner that the magnetic field produced by the magnets be as uniform as possible. The uniform magnetic field keeps the charged particle or ion in a spiral path while travelling between the hollow D-shaped electrodes. The magnetic field is directed perpendicular to the electric field as a result the ion experiences a Lorentz force perpendicular to the radius of the spiral path and therefore moves in a circular path.

Dynamic electric field

The dynamic electric field is implemented using a radio frequency generator which induces an alternating current across the pair of hollow metallic D-shaped electrodes. The frequency of the alternating current is adjusted depending on the frequency of the rotation of the ion inside the D-shaped electrodes. The frequency is very important for the ions to attain maximum energy in the minimum number of turns and is thus called the frequency of that cyclotron. When the electrons travel through the diametral gap between the electrodes, they experience an electrostatic force and thus attain a higher energy. An alternating radio frequency is required to change the direction of the electric field after every half-rotation of the ion across the electrodes. After attaining a higher energy, the ion rotates with a larger radius. This dynamic electric field powers the resonance principle which is the driving power behind the working of a cyclotron.

Construction of A Cyclotron

A basic cyclotron works by accelerating charged particles in a spiral path inside the cyclotron inside a pair of electrodes. The electrodes are a pair of hollow semi-circular flat metallic cylinders in the shape of a capital “D” and are thus called “dees”. The charged particles or ions revolve in order to attain a high energy state even with a much lower applied voltage. These dees are so constructed that it is possible to evacuate the air from them during operation as the collisions of the bombarding particles with air molecules greatly decreases the energy of the particles. The electrodes are connected to a radio frequency generator and are placed in a nearly uniform magnetic field. Charged particles are produced by an ion source directly in the centre of the cyclotron between the two electrodes. The dees are located between the poles of electromagnet. The alternating current field applied by the magnet causes the charged ions to revolve inside the dees with increasing velocity and kinetic energy. These dees are connected to a radio frequency generator and are placed in a nearly uniform magnetic field. The magnetic field causes the particle to move in the median plane in approximately circular orbits inside the hollow electrodes and across the gap between them. At each gap, particles are accelerated and, therefore, they follow a spiral path as they gain energy.

Cyclotron magnets are classically simple in their design features. Most preferably electromagnets are used for their ability of fine tuning the required magnetic field. The magnets are aligned horizontally perpendicular to the electric field. This arrangement powers the resonance principle which is the main principle behind the working of a cyclotron, keeping the charged particle inside the electrodes traveling in a spiral circular path. This helps in accelerating the ion multiple times without requiring large sized particle accelerators.

The D-shaped electrodes are kept in a chamber, which fits between the poles of the electromagnet. The chamber must be vacuum-tight, which is necessary since without the vacuum the ions will experience resistance from the air molecules when travelling at high velocities, and the chamber is mechanically designed with adequate structural strength to resist distortion when under vacuum. It is constructed of non-magnetic materials to prevent disturbance of the symmetrical magnetic field and are of high electrical conductivity to provide low resistance for the radio frequency currents.

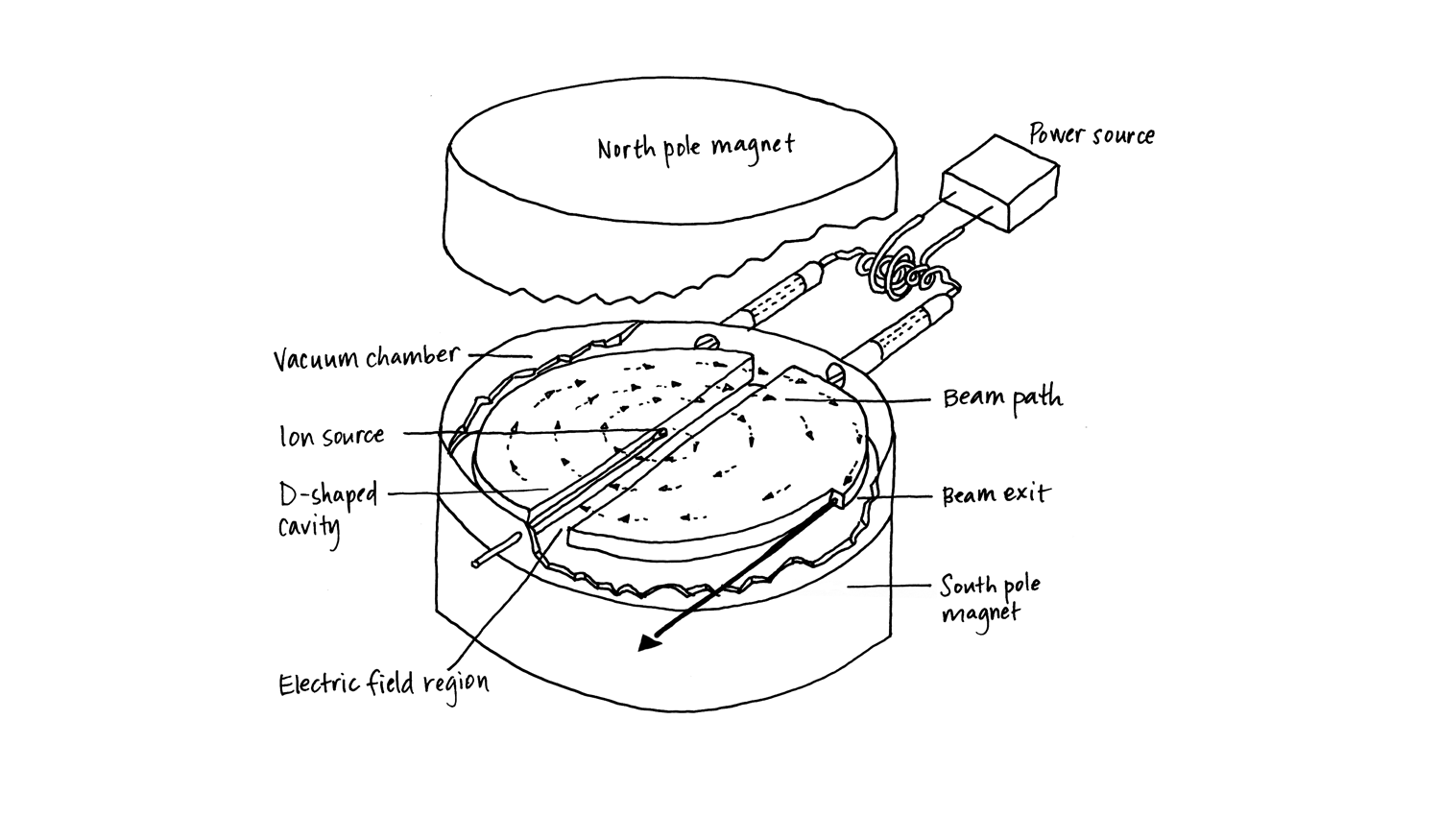
Fig.4 - Construction of a cyclotron
Fig.4 - Construction of a cyclotron

Explanation of Working of a Cyclotron

There are two forces behind the working of a cyclotron: the dynamic electric field and the static magnetic field. The electric field is provided by the two hollow D-shaped electrodes separated by a diametral gap inside the vacuum chamber, while the magnetic field is produced by the two powerful magnets (preferably electromagnets) located above and below the hollow electrodes. This whole setup is enclosed in a tightly packed vacuum chamber to avoid any loss of energy arising from the friction provided by air resistance.

This arrangement of the hollow electrodes and the magnets inside the vacuum chamber provides the cyclotron with the characteristic resonance principle. The north pole of the magnet is placed above the electrodes and the south pole is placed below them, therefore the net magnetic field acts across the electrode in the downwards direction. While the electric field acts from the positive electrode to the negative electrode in the region of the diametral gap (since, there is no electric field inside a conductor). The polarity of the electrodes as well as the direction of the electric field changes back and forth due to the alternating current applied to the electrodes.

The charged particle or the ion which is to be accelerated is ejected near the centre of the vacuum chamber between the electrodes in the region of the diametral gap. As soon as the ion is ejected it is attracted by the oppositely charged electrode at that instant due to the electrostatic forces. The ion accelerates and enters the electrode. The region inside the D-shaped electrode being electric-field-free zone, the ions are not accelerated but are acted upon only by a near uniform magnetic field which forces it to travel in circular orbits in a plane normal to the magnetic field.

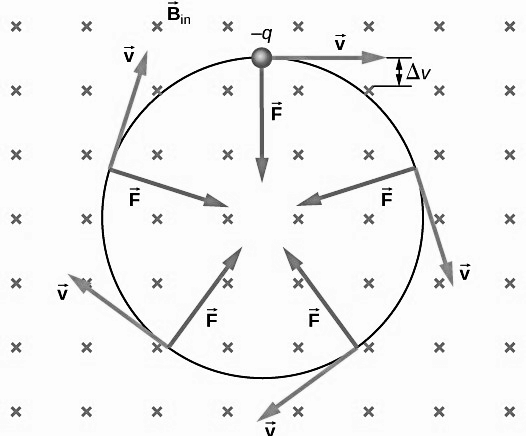
The magnetic field drives the ions to be in a circular path due to the Lorentz force applied due to the presence of the magnetic field and the charge on the ions. The Lorentz force is applied perpendicular to the radius of rotation of the particle as a result the particle moves in a circular path.

After traversing a semi-circular path, the ions return to the diametral gap between the electrodes and come in the influence of the electric field. For the condition of resonance, the magnetic field is adjusted so the time required for ions to complete a semicircle is equal to the time for reversal of the oscillatory electric field. Therefore, after traversing the first semi-circle the ion experiences another acceleration due to the electrostatic forces, acquiring a higher velocity, and goes onto travel a path of larger radius within the other electrode. As long as the resonance is maintained, the ions are accelerated each time it crosses the diametral gap, travelling in ever-widening semicircles until it reaches the periphery of the electrodes and gets ejected out of the cyclotron with an enormous energy.

The frequency of the alternating current is very crucial for the charged particles to be in complete phase so that they can attain very high energies with the minimum number of turns. If the frequency of the cyclotron is not fine-tuned for the ion to be in phase the efficiency of the cyclotron decreases drastically.

Fig.5 - Vector diagram of the forces acting inside the cyclotron on an electron
Fig.5 - Vector diagram of the forces acting inside the cyclotron on an electron

Mathematical Explanation of Working of a Cyclotron

Magnetic Field of a cyclotron

The magnetic field provides the Lorentz force on the ions, which is equivalent to,

\[\vec{F}=q(\vec{v}\times\vec{B})\]

where,
\(\vec{F}\) represents the magnetic force on the ion;
\(q\) represents the charge on the ion;
\(\vec{v}\) represents the velocity of the ion;
\(\vec{B}\) represents the magnetic field of the cyclotron.

Because the direction of the force is the cross product between the velocity of the particle and the magnetic field, the Lorentz force is perpendicular to both. Since the accelerated ions travel in a plane normal to the magnetic field, the magnitude of the Lorentz force is,

\[F=qvB\]

This magnetic force causes the ion to travel in a circular path, if \(m\) is the mass of the ion and \(r\) is the radius of the circular orbit. Then the centripetal force acting on the ion is,

\[F=\frac{mv^2}{r}\]

Comparing the centripetal force with the Lorentz magnetic force, we get,

\[qvB=\frac{mv^2}{r}\]

Electric Field of a cyclotron

The oscillating electric field supplies the force to accelerate the particles to high velocities. As the ions travel in a circular path in a magnetic field, they will cross the gap between the two D-shaped electrodes twice in a revolution, each time receiving an electrostatic force accelerating them to a higher energy.

The force acting on the particles with charge \(q\) and electric field \(E\) is,

\[\vec{F_E}=q\vec{E}\]

Frequency of a cyclotron

The frequency of revolution \(f\) of the ion in the circular path is,

\[f=\frac{v}{2\pi r}=\frac{qB}{2\pi m}\]

This frequency \(f\) is thus constant for a uniform electric field \(B\) as long as the mass \(m\) and charge \(q\) of the ion is constant. Thus, the relation between \(f\) and \(B\) becomes,

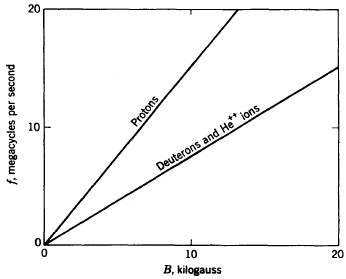
\[f=\left(\frac{1}{2\pi}\times \frac{q}{m}\right)\times B\]

This linear relation between applied frequency and magnetic field is the fundamental equation of cyclotron resonance. When evaluated for the \(q/m\) values characteristic of light ions, we get

Ions \(f\)(megacycles)
protons (\(H^+\)) \(1.52B\)
deuterons (\(D^+\)) \(0.76B\)
\(\alpha\)-particle (\(He^{++}\)) \(0.76B\)

The above relations are plotted in graph to illustrate the range of frequencies required to produce resonant acceleration in magnetic fields up to 20 kilogauss.

Graph 1 - Demonstrating variation of frequency between various charged particles
Graph 1 - Demonstrating variation of frequency between various charged particles

Velocity of an ion in a cyclotron

Comparing the centripetal force with the Lorentz force, we get,

\[\frac{mv^2}{r}=qvB\] \[\implies v^2 = qvB \times \frac{r}{m}\] \[\implies v=\sqrt{qvB \times \frac{r}{m}}\]

Energy of an ion in a cyclotron

Considering the average potential difference between the two D-shaped electrodes be \(V\). The increment in the kinetic energy (\(\Delta E_K\)) for each traversal through the diametral gap would be,

\[\Delta E_K = qV\]

Considering the ion accelerates \(n\) times by passing through the diametral gap, the total kinetic energy (\(E_K\)) processed by the ion during the final rotation would be,

\[E_K = n \times qV\]

But, \(n=\left(\frac{f}{2}\right)\)

\[E_K = \left(\frac{f}{2}\right) \times qV\]

Considering the velocity of the ion during the final rotation be \(v\), the total kinetic energy (\(E_K\)) processed by the ion would be,

\[E_K = n \times qV = \frac{1}{2}mv^2\]

Therefore, the output kinetic energy of the particles expressed in terms of the magnetic field \(B\) and final orbit radius \(R\),

\[E_K = \frac{q^2B^2R^2}{2m}\]

Expressing the kinetic energy per unit charge,

\[\frac{E_K}{q} = \frac{1}{2}\frac{q}{m}B^2R^2\]

Voltage-Time relation of a cyclotron

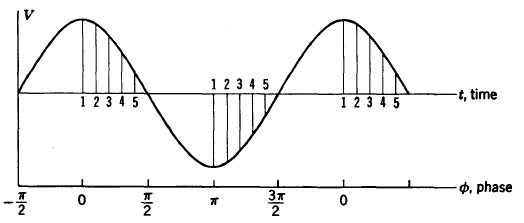
A voltage-time graph of the potential between the electrodes of a cyclotron is shown in the graph. On each traversal of the diametral gap between electrodes the particle will acquire an increment of kinetic energy, \(\Delta E_K = qV\), where \(V\) is the potential difference between the two electrodes. The magnitude of the increment is determined by the phase of crossing the gap. Since, the particles will be moving in opposite directions in successive passages through the diametral gap, so the kinetic energy increments are cumulative. Distinct phases of resonance are plotted on the graph (\(points - 1, 2, 3, 4 ...\)), a resonant particle crossing at the phase of peak field (\(point - 1\)) will reach maximum energy in the minimum number of turns. While the ions crossing at other phases (\(points - 2, 3, 4 ...\)), will acquire energy in smaller increments but will remain in resonance for a larger number of turns to reach the maximum energy.

Graph 2 - Voltage-time relation of a cyclotron
Graph 2 - Voltage-time relation of a cyclotron

Advantages of Cyclotrons

Cyclotron was a huge improvement over the previous generation particle accelerators for several reasons:

Limitations of Cyclotrons

When professor Lawrence invented the cyclotron, he did not consider the relativistic consequences. He assumed the spiral path of the particle inside the cyclotron was in accordance with Newton’s laws of motion. If the particles acquire enough energy so to become sufficiently fast that the relativistic effects become more important then the desired results are not obtained. At high velocities, the mass of the particle increases according to the given formula,

\[m=\frac{m_0}{\sqrt{1-\frac{v^2}{c^2}}}\]

where,
\(m\) represents the mass of the particle at the instant when velocity is \(v\);
\(m_0\) represents the rest mass of the particle;
\(c\) represents the speed of light.

This change in mass largely affects the performance of the cyclotron. Apart from the relativistic consequences, cyclotrons are also unable to accelerate electrons because they have very low mass and get energised rapidly. The velocity of the cyclotron increases to such a great extent that the electron will be thrown out of the step with the oscillating field.

Modifications of Cyclotron

In order to correct the relativistic limitations of a cyclotron some adjustments are made to the original design of the cyclotron by Professor Lawrence. The following are some special types of cyclotron classified based on the adjustments made to the original design.

The adjustments were made using the adjustment factor \(\gamma\),

\[\gamma = \frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\]

Synchrocyclotron

Instead of a constant frequency in an original cyclotron, the frequency of the RF electric field in a synchrocyclotron is varied to compensate for the relativistic effects on the mass of the particles as its velocity approaches the speed of light.

The frequency is adjusted using the following equation,

\[f=\frac{f_0}{\gamma}\]

where,
\(f\) represents the frequency of the synchrocyclotron;
\(f_0\) represents the frequency of the non-adjusted cyclotron;
\(\gamma\) represents the Lorentz factor.

Isochronous cyclotron

Isochronous cyclotron is an alternative to the synchrocyclotron, in this design the magnetic field increases with the radius. Isochronous cyclotrons can produce particles with much greater velocity compared to synchrocyclotrons.

The magnetic field is adjusted using the following equation,

\[B=\gamma B_0\]

where,
\(B\) represents the magnetic field of the isochronous cyclotron;
\(B_0\) represents the magnetic field of the non-adjusted cyclotron;
\(\gamma\) represents the Lorentz factor.

Conclusion

Cyclotron was invented in 1930 by Ernest Orlando Lawrence. It revolutionised the way particle accelerators worked. It provided a very efficient design for accelerating charged particles to very high speeds with a fraction of voltage applied across electrodes. The circular design of the cyclotron made it very compact. Cyclotrons are preferred over other cyclotrons for its efficiency.

Before cyclotrons, charged particles were accelerated mostly using linear particle accelerators. Linear particle accelerators used multiple electric fields to accelerate the particles making the design very bulky. Cyclotron solved this problem by giving a compact circular design which was able to accelerate particles to high velocity by accelerating them in the same electric field repeatedly.

The cyclotron resonance principle worked with the help of a static magnetic field and an alternating electric field. The static magnetic field keeps the charged particle in its orbit inside the electrodes, whereas the alternating current across the electrodes is used to accelerate the particles by revolving them in a spiral trajectory of increasing radius. The particle keeps on gaining energy and therefore increases its radius every time there is an increase in its velocity. Ultimately when the radius of its trajectory becomes equal to the radius of the cyclotron it is ejected as a beam of very high current.

Though cyclotron was a huge improvement over its predecessors, it still had some drawbacks. The design of cyclotron did not consider the relativistic effects of high velocity in the mass of the particles. Therefore, later some adjustments were made to cancel the relativistic effects.

Cyclotron paved a way for a new generation of particle accelerators. It solved many problems associated with previous accelerators. It revolutionised the way particle accelerators worked by putting forward the resonance principle.

Bibliography